MATH 2100 C958 Calculus I

Access The Exact Questions for MATH 2100 C958 Calculus I

💯 100% Pass Rate guaranteed

🗓️ Unlock for 1 Month

Rated 4.8/5 from over 1000+ reviews

  • Unlimited Exact Practice Test Questions
  • Trusted By 200 Million Students and Professors

130+

Enrolled students
Starting from $30/month

What’s Included:

  • Unlock Actual Exam Questions and Answers for MATH 2100 C958 Calculus I on monthly basis
  • Well-structured questions covering all topics, accompanied by organized images.
  • Learn from mistakes with detailed answer explanations.
  • Easy To understand explanations for all students.
Subscribe Now payment card

Rachel S., College Student

I used the Sales Management study pack, and it covered everything I needed. The rationales provided a deeper understanding of the subject. Highly recommended!

Kevin., College Student

The study packs are so well-organized! The Q&A format helped me grasp complex topics easily. Ulosca is now my go-to study resource for WGU courses.

Emily., College Student

Ulosca provides exactly what I need—real exam-like questions with detailed explanations. My grades have improved significantly!

Daniel., College Student

For $30, I got high-quality exam prep materials that were perfectly aligned with my course. Much cheaper than hiring a tutor!

Jessica R.., College Student

I was struggling with BUS 3130, but this study pack broke everything down into easy-to-understand Q&A. Highly recommended for anyone serious about passing!

Mark T.., College Student

I’ve tried different study guides, but nothing compares to ULOSCA. The structured questions with explanations really test your understanding. Worth every penny!

Sarah., College Student

ulosca.com was a lifesaver! The Q&A format helped me understand key concepts in Sales Management without memorizing blindly. I passed my WGU exam with confidence!

Tyler., College Student

Ulosca.com has been an essential part of my study routine for my medical exams. The questions are challenging and reflective of the actual exams, and the explanations help solidify my understanding.

Dakota., College Student

While I find the site easy to use on a desktop, the mobile experience could be improved. I often use my phone for quick study sessions, and the site isn’t as responsive. Aside from that, the content is fantastic.

Chase., College Student

The quality of content is excellent, but I do think the subscription prices could be more affordable for students.

Jackson., College Student

As someone preparing for multiple certification exams, Ulosca.com has been an invaluable tool. The questions are aligned with exam standards, and I love the instant feedback I get after answering each one. It has made studying so much easier!

Cate., College Student

I've been using Ulosca.com for my nursing exam prep, and it has been a game-changer.

KNIGHT., College Student

The content was clear, concise, and relevant. It made complex topics like macronutrient balance and vitamin deficiencies much easier to grasp. I feel much more prepared for my exam.

Juliet., College Student

The case studies were extremely helpful, showing real-life applications of nutrition science. They made the exam feel more practical and relevant to patient care scenarios.

Gregory., College Student

I found this resource to be essential in reviewing nutrition concepts for the exam. The questions are realistic, and the detailed rationales helped me understand the 'why' behind each answer, not just memorizing facts.

Alexis., College Student

The HESI RN D440 Nutrition Science exam preparation materials are incredibly thorough and easy to understand. The practice questions helped me feel more confident in my knowledge, especially on topics like diabetes management and osteoporosis.

Denilson., College Student

The website is mobile-friendly, allowing users to practice on the go. A dedicated app with offline mode could further enhance usability.

FRED., College Student

The timed practice tests mimic real exam conditions effectively. Including a feature to review incorrect answers immediately after the simulation could aid in better learning.

Grayson., College Student

The explanations provided are thorough and insightful, ensuring users understand the reasoning behind each answer. Adding video explanations could further enrich the learning experience.

Hillary., College Student

The questions were well-crafted and covered a wide range of pharmacological concepts, which helped me understand the material deeply. The rationales provided with each answer clarified my thought process and helped me feel confident during my exams.

JOY., College Student

I’ve been using ulosca.com to prepare for my pharmacology exams, and it has been an excellent resource. The practice questions are aligned with the exam content, and the rationales behind each answer made the learning process so much easier.

ELIAS., College Student

A Game-Changer for My Studies!

Becky., College Student

Scoring an A in my exams was a breeze thanks to their well-structured study materials!

Georges., College Student

Ulosca’s advanced study resources and well-structured practice tests prepared me thoroughly for my exams.

MacBright., College Student

Well detailed study materials and interactive quizzes made even the toughest topics easy to grasp. Thanks to their intuitive interface and real-time feedback, I felt confident and scored an A in my exams!

linda., College Student

Thank you so much .i passed

Angela., College Student

For just $30, the extensive practice questions are far more valuable than a $15 E-book. Completing them all made passing my exam within a week effortless. Highly recommend!

Anita., College Student

I passed with a 92, Thank you Ulosca. You are the best ,

David., College Student

All the 300 ATI RN Pediatric Nursing Practice Questions covered all key topics. The well-structured questions and clear explanations made studying easier. A highly effective resource for exam preparation!

Donah., College Student

The ATI RN Pediatric Nursing Practice Questions were exact and incredibly helpful for my exam preparation. They mirrored the actual exam format perfectly, and the detailed explanations made understanding complex concepts much easier.

Ace Your Test with MATH 2100 C958 Calculus I Actual Questions and Solutions - Full Set

Free MATH 2100 C958 Calculus I Questions

1.

Using simpson's rule ​​​​​​​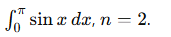

  • 2

  • 1.9

  • 2.1

  • 0

Explanation

​​​​​​​


2.

Area between y = sin⁡ x and y = cos ⁡x from 0 to π/4?​​​​​​​

  • √2​−1

  • 1

  • √2/2

  • 0

Explanation

​​​​​​​​​​​​​​


3.

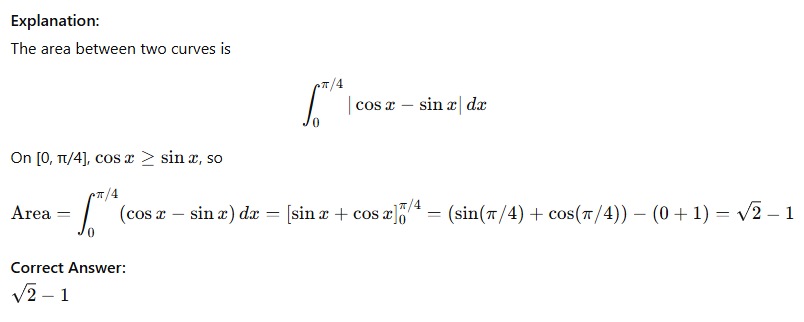
Higher derivative: 4th derivative of f(x) = e−x?

  • e−x

  • −e−x

  • ex

  • 0

Explanation

​​​​​​​


4.

A teacher demonstrates squeeze theorem: if x2 ≤  sin⁡x/x ≤ 1 near 0, what is lim⁡x→0sin⁡ x/x​?

  • 0

  • 1

  • ∞

  • -1

Explanation

Explanation:

By the squeeze theorem, if a function is "sandwiched" between two other functions that have the same limit at a point, then the function also approaches that limit. Here, as x → 0, x2→ 0 and the constant 1 is 1. The standard limit lim⁡ x→0 sin⁡x/x​ is well-known to be 1. Therefore, despite the inequality given, the actual limit is determined by the behavior of sin⁡x/x near 0.

​​​​​​​Correct Answer:

1


5.

Related rates: cone height decreases at 1 cm/s, radius fixed at 3 cm, volume rate when h = 4?

  • −12π cm3/s

  • −9π cm3/s

  • −36π cm3/s

  • −3π cm3/s

Explanation

​​​​​​​


6.

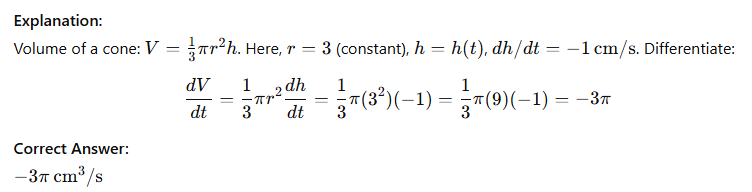
Derivative of f(x) = cot⁡−1(x2)?

  • ​​​​​​​ ​​​​​​​ ​​​​​​​

  • ​​​​​​​

  • ​​​​​​​

  • ​​​​​​​

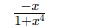
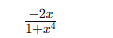
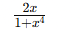
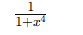
Explanation

​​​​​​​


7.

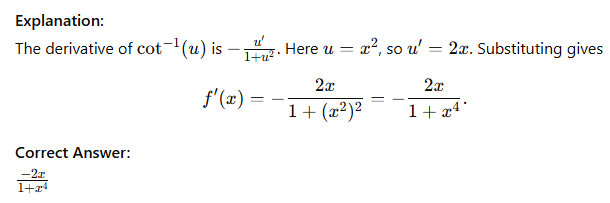
A student asks: “Why do we need the chain rule?” The teacher responds it is used when:

  • Differentiating a composite function

  • Finding critical points

  • Evaluating definite integrals

  • Applying L’Hôpital’s rule

Explanation

Explanation:

The chain rule is a fundamental rule in calculus used to differentiate composite functions. If a function can be expressed as f(g(x)), where one function is nested inside another, the derivative is found by multiplying the derivative of the outer function evaluated at the inner function by the derivative of the inner function: d/dx [f`(g(x))] = f'(g(x)).g'(x). This allows us to handle more complex functions that cannot be differentiated directly using simple rules.

​​​​​​​Correct Answer:

Differentiating a composite function


8.

In a lesson on substitution: ∫ln⁡x/x dx = ?

  • (ln⁡x)2 + C

  • 1/2(ln⁡x)2 + C

  • ln⁡∣ln⁡x∣ + C

  • x ln⁡x + C

Explanation

​​​​​​​


9.

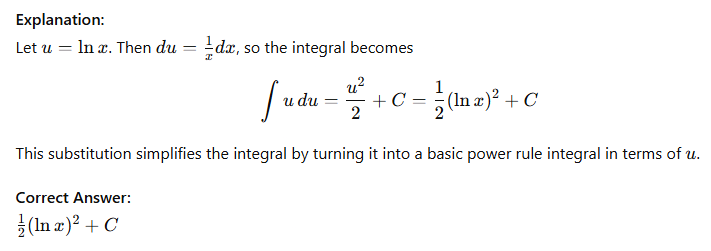
A teacher analyzes f(x) = x2− 4x + 3. Where is it increasing?

  • x < 1 or x > 3

  • 1 < x < 3

  • Everywhere

  • x > 2

Explanation

​​​​​​​


10.

Volume by shells: rotate y = x2 from 0 to 1 about y-axis?

  • 2π/5

  • π/5

  • 2π/3

  • π/2

Explanation

​​​​​​​


How to Order

1

Select Your Exam

Click on your desired exam to open its dedicated page with resources like practice questions, flashcards, and study guides.Choose what to focus on, Your selected exam is saved for quick access Once you log in.

2

Subscribe

Hit the Subscribe button on the platform. With your subscription, you will enjoy unlimited access to all practice questions and resources for a full 1-month period. After the month has elapsed, you can choose to resubscribe to continue benefiting from our comprehensive exam preparation tools and resources.

3

Pay and unlock the practice Questions

Once your payment is processed, you’ll immediately unlock access to all practice questions tailored to your selected exam for 1 month .

Subscribe Now