C646 Trigonometry and Precalculus
Access The Exact Questions for C646 Trigonometry and Precalculus
💯 100% Pass Rate guaranteed
🗓️ Unlock for 1 Month
Rated 4.8/5 from over 1000+ reviews
- Unlimited Exact Practice Test Questions
- Trusted By 200 Million Students and Professors
What’s Included:
- Unlock Actual Exam Questions and Answers for C646 Trigonometry and Precalculus on monthly basis
- Well-structured questions covering all topics, accompanied by organized images.
- Learn from mistakes with detailed answer explanations.
- Easy To understand explanations for all students.

Access and unlock Multiple Practice Question for C646 Trigonometry and Precalculus to help you Pass at ease.
Free C646 Trigonometry and Precalculus Questions
A surveyor needs to calculate the height of a building. They stand a distance x away from the base of the building and measure the angle of elevation to the top as π/6 radians. If the distance x is 30 meters, what is the height of the building?
-
30√3 meters
-
10√3 meters
-
15 meters
-
10 meters
Explanation

Explain in your own words why the limit of a rational function, as x approaches infinity, is the ratio of the leading coefficients when the degree of the numerator and denominator are the same.
-
The constant terms become significant as x approaches infinity.
-
The function oscillates rapidly, and the ratio represents the average value.
-
As x becomes very large, the terms with the highest degree dominate the function's behavior, making the ratio of their coefficients the determining factor for the limit.
-
The limit is always zero in this case
-
The lower degree terms cancel each other out, leaving only the leading coefficients.
Explanation
When x becomes extremely large, the highest-degree terms in both the numerator and denominator grow far faster than any lower-degree terms or constants. Because these dominant terms dictate the overall behavior of the function, all smaller terms become negligible. Therefore, the limit depends solely on how the leading terms compare, and the ratio of their coefficients determines the limit of the entire rational function.
In polar coordinate conversions, what trigonometric function is associated with the x-coordinate?
-
Tangent
-
Sine
-
Secant
-
Cosine
Explanation
In polar coordinates, a point is represented as (r, θ), where r is the distance from the origin and θ is the angle from the positive x-axis. The Cartesian x-coordinate is given by (x = r \cos(\theta)), directly associating the x-coordinate with the cosine function. This comes from projecting the point onto the horizontal axis using the angle θ.
Explain in your own words what the derivative f'(c) represents geometrically, based on the limit definition f'(c) = lim(x→c) [f(x) - f(c)] / (x - c).
-
The slope of the tangent line to the graph of f(x) at the point (c, f(c)).
-
The average rate of change of f(x) over the entire domain.
-
The area under the curve of f(x) from 0 to c.
-
The instantaneous velocity of an object at time c, where f(x) represents position.
Explanation
The derivative f'(c) is defined as the limit of the difference quotient as x approaches c. Geometrically, this represents the slope of the tangent line to the curve of f(x) at the point (c, f(c)), showing how steeply the function is increasing or decreasing at that exact point.
In the context of logistic growth, as modeled by the equation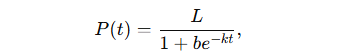 what does L represent?
what does L represent?
-
Population at time t
-
Carrying capacity
-
Time elapsed
-
Growth rate constant
-
Initial population size
Explanation
According to the limit rules for rational functions, what is the limit as x approaches infinity if the degree of the numerator is greater than the degree of the denominator?
-
1
-
0
-
Infinite or Does Not Exist (DNE)
-
Cannot be determined
-
The ratio of the leading coefficients
Explanation
For a rational function where the numerator has a higher degree than the denominator, the numerator grows much faster than the denominator as x approaches infinity. This causes the value of the function to increase without bound. Therefore, the limit does not approach a finite number and is considered infinite or does not exist (DNE).
Explain in your own words why the formula dy/dx = (dy/dθ) / (dx/dθ) is used to find the slope of a tangent line in polar coordinates, relating it to the chain rule.
-
The formula represents the inverse relationship between x and y in polar form.
-
The formula is an application of the chain rule, where the rate of change of y with respect to x is found by dividing the rate of change of y with respect to θ by the rate of change of x with respect to θ.
-
The formula is a simplification of the limit definition of the derivative in polar coordinates.
-
The formula directly calculates the slope using Cartesian coordinates converted to polar form.
-
The formula is derived from the Pythagorean theorem applied to polar coordinates.
Explanation
In polar coordinates, both x and y are expressed as functions of θ: x = r cos(θ) and y = r sin(θ). To find the slope of a tangent line dy/dx, we need the derivative of y with respect to x. Using the chain rule, dy/dx can be expressed as (dy/dθ) / (dx/dθ), which divides the rate of change of y with respect to θ by the rate of change of x with respect to θ. This method efficiently converts polar derivatives into Cartesian slopes and is directly based on the chain rule in calculus.
Explain in your own words what the constant 'C' represents in the integral formula ∫ du / (u√(u² - a²)) = 1/a arcsec |u|/a + C.
-
C represents the limit of the function as u approaches infinity.
-
C represents the initial value of u.
-
C represents the constant of integration, accounting for the fact that the derivative of a constant is zero.
-
C represents the circumference of a circle with radius 'a'.
-
C represents the value of 'a' when u is zero.
Explanation
In an indefinite integral, the result represents a family of functions whose derivatives equal the integrand. Since the derivative of any constant is zero, adding a constant does not change the derivative. The '+ C' in the integral formula ensures that all possible antiderivatives are included, accounting for the fact that the original function could differ by any constant value.
A particle's position is given by the function s(t) = 3t² + 2t. Using the limit definition of the derivative, find the instantaneous velocity of the particle at t = 2.
-
16
-
10
-
12
-
8
-
14
Explanation
The instantaneous velocity is the derivative of the position function s(t) with respect to time. Using the standard derivative rules (or the limit definition), ds/dt = d/dt (3t² + 2t) = 6t + 2. Substituting t = 2 gives v(2) = 6(2) + 2 = 12 + 2 = 14. Thus, the particle's instantaneous velocity at t = 2 is 14.
Explain in your own words what it means for a series (\Sigma a_n) to converge absolutely, and why this is a stronger condition than just convergence.
-
Absolute convergence means that both Σa_n and Σ|a_n| diverge, implying the series is unstable.
-
Absolute convergence means that the terms a_n approach zero very slowly
-
Absolute convergence means that the series Σa_n converges, but Σ|a_n| diverges, indicating conditional convergence.
-
Absolute convergence means that the series Σ|a_n| converges, implying that the original series Σa_n also converges, and is more robust to rearrangement of terms.
Explanation
A series Σan converges absolutely if the series of absolute values Σ|an| converges. This is a stronger condition than ordinary convergence because absolute convergence guarantees that the original series Σan converges regardless of the signs of its terms. Moreover, absolutely convergent series are stable under rearrangements, whereas conditionally convergent series can change their sum if terms are reordered.
How to Order
Select Your Exam
Click on your desired exam to open its dedicated page with resources like practice questions, flashcards, and study guides.Choose what to focus on, Your selected exam is saved for quick access Once you log in.
Subscribe
Hit the Subscribe button on the platform. With your subscription, you will enjoy unlimited access to all practice questions and resources for a full 1-month period. After the month has elapsed, you can choose to resubscribe to continue benefiting from our comprehensive exam preparation tools and resources.
Pay and unlock the practice Questions
Once your payment is processed, you’ll immediately unlock access to all practice questions tailored to your selected exam for 1 month .